प्रायिकता वितरण

द्विपद प्रायिकता वितरण

एक यादृच्छिक चर (Random Variable ) द्विपद बंटन का अनुसरण करता है यदि

1. यादृच्छिक चर असतत है
2. यादृच्छिक चर को निश्चित संख्या में देखा जाता है (एक सिक्के को उछालने और परिणाम देखने की कल्पना करें)
3. केवल दो संभावित परिणाम हैं। कोई उन्हें 0 या 1 या सफलता या विफलता या सही या गलत के रूप में लेबल कर सकता है
4. प्रत्येक परिणाम से जुड़ी प्रायिकताएँ होती हैं जिनका योग 1 होता है। यदि सफलता की प्रायिकता p है, तो विफलता की प्रायिकता (1-p) है।
5. प्रत्येक परिणाम दूसरे से स्वतंत्र होता है।

n के यादृच्छिक चयन से y सफलताओं की प्रायिकता है

\[ P(y)=_nC_yp^y(1-p)^{n-y} \]

जहाँ y सफलता की संख्या है, p सफलता की प्रायिकता है और n नमूना आकार (संख्या ) है।

R में, कोई dbinom फ़ंक्शन का उपयोग करके प्रायिकता की गणना कर सकता है। मान लीजिए कि आप जानते हैं कि पेनल्टी शूटआउट में मेसी ने 77% बार स्कोर किया है। इस जानकारी को देखते हुए, आप यह समझना चाहते हैं कि यदि मेस्सी 5 पेनल्टी किक लेता है, तो क्या संभावना है कि उनमें से तीन गोल होंगे।

dbinom(3,5,0.77)

## [1] 0.241506

हमें इस संभावना के बारे में यदि यह पूछा जाय कि गोल की संख्या 3 से अधिक नहीं होने की सम्भावना कितनी है ? इसे करने के दो तरीके हैं। पहले तरीके में, हम ०,१,२ और ३ गोलों की प्रायिकताएँ जोड़ते हैं।

sum(dbinom(0:3,5,0.77))

## [1] 0.3250616

दूसरे में, हम एक अन्य फ़ंक्शन pbinom का उपयोग करते हैं

pbinom(3,5,0.77)

## [1] 0.3250616

वितरण का माध्य नमूना आकार प्रायिकता का गुणा है। हमारे उदाहरण में, हम 5 किक में से औसतन 5*0.77 (3.85) गोल की उम्मीद कर सकते हैं। मानक विचलन \(\sqrt{np(1-p)}\) है।

पॉसों प्रायिकता वितरण

जब भी हम एक अंतराल में एक असतत चर के किसी विशेष परिणाम की घटनाओं की संख्या से निपटते हैं, जिसके लिए घटनाओं की औसत संख्या ज्ञात होती है, तो हम पॉइज़न का उपयोग करते हैं। उदाहरण के लिए, प्रति दिन एक दुकान पर आने वाले ग्राहकों की संख्या या एक महीने में मेस्सी द्वारा लक्ष्यों की संख्या। अंतराल समय, स्थान या आयतन हो सकता है। उदाहरण के लिए, एक तालाब से प्रति लीटर पानी में जीवों की संख्या।

y घटनाओं की प्रायिकता या अंतराल में किसी विशेष परिणाम के अवलोकन द्वारा दिया जाता है

\[ P(y)=\frac{e^{-a}a^y}{y!} \] जहां a अंतराल में किसी विशेष परिणाम की घटनाओं या टिप्पणियों की औसत संख्या है।

द्विपद में फंक्शन्स के समान, आर में भी पॉइसन के लिए कार्य हैं।

यह मानते हुए कि मेस्सी हर 1 मैच में औसतन 2 गोल करता है, हम इस संभावना की गणना करना चाहते हैं कि हम अगले 1 मैच में 2 गोल देखेंगे?

dpois(1,2)

## [1] 0.2706706

यदि हम कम से कम एक लक्ष्य के अवलोकन की प्रायिकता जानना चाहते हैं, तो इसके दो तरीके हैं। हम 0 और 1 लक्ष्य की संभावनाओं को जोड़ सकते हैं या ppois फ़ंक्शन का उपयोग कर सकते हैं।

sum(dpois(0:1,2))

## [1] 0.4060058

ppois(1,2)

## [1] 0.4060058

वितरण का माध्य a के बराबर होता है जो पहले से ही ज्ञात है। मानक विचलन \(\sqrt{a}\) . है

सामान्य संभाव्यता वितरण

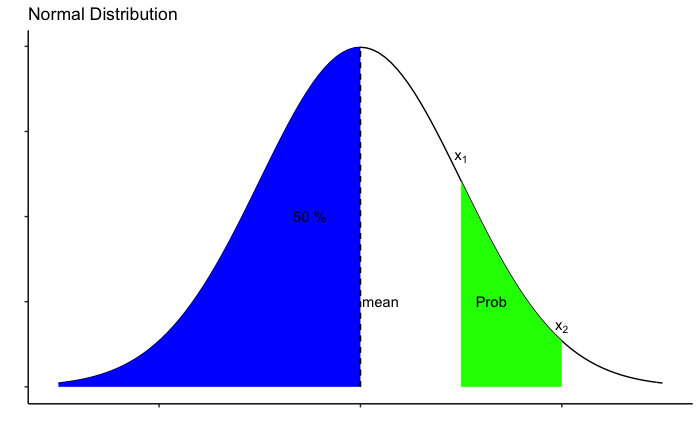
सामान्य संभाव्यता वितरण है

1. बेल के आकार का वक्र
2. माध्य के बारे में सममित, जो केंद्रीय मान है
3. पूँछ जो कभी भी x-अक्ष को स्पर्श नहीं करती (स्पर्शोन्मुख)
4. वितरण को दो मापदंडों, माध्य और मानक विचलन द्वारा वर्णित किया जा सकता है
5. वक्र के अंतर्गत कुल क्षेत्रफल 1 और . है
6. अंतराल की प्रायिकता, अंतराल परिसर के वक्र के नीचे का क्षेत्र है

library(ggplot2)
ggplot(data.frame(x = c(-3, 3)), aes(x)) +
  stat_function(fun = dnorm) + 
  stat_function(fun = dnorm, 
                xlim = c(-3,0),
                geom = "area",
                fill="blue") +
    stat_function(fun = dnorm, 
                xlim = c(1,2),
                geom = "area",
                fill="green")+
  labs(
    title = "(Standard)Normal Distribution",
    x="",
    y=""
  ) +
  geom_segment(x=0, xend=0, y=0, yend=0.4, linetype="dashed") +
  annotate("text", x=1, y=0.27, label=expression(x[1]))+
  annotate("text", x=2, y=0.07, label=expression(x[2]))+
  annotate("text", x=1.3, y=0.1, label="Prob")+
  annotate("text", x=0.2, y=0.1, label="mean=0")+
  annotate("text", x=-0.5, y=0.2, label="50 %")+
theme_classic() +
  theme(axis.text.x = element_blank(),
        axis.text.y = element_blank()
        ) 

मानक सामान्य विचलन की संभावनाएं z-तालिका नामक तालिका में उपलब्ध हैं। चूंकि तालिका मानक की संभावनाएं प्रदान करती है, हम यादृच्छिक चर (x) को z-मान में परिवर्तित करते हैं।

\[ z=\frac{x-\mu}{\sigma} \] z-value मूल रूप से x अक्ष में चर के विशेष मान की स्थिति को इंगित करता है (माध्य से कितनी दूर)।

आर में, ‘जेड-टेबल’ का उपयोग करने की कोई आवश्यकता नहीं है। ऐसे फंक्शन्स हैं, जैसे द्विपद और पॉइसन के मामले में, जो गणना में मदद कर सकते हैं।

मान लीजिए कि एक कक्षा में विद्यार्थियों के भार का माध्य 50 और मानक विचलन 5 है। हम कक्षा में शीर्ष 15% भारों की निचली सीमा जानना चाहते हैं।

ggplot(data.frame(x = c(-3, 3)), aes(x)) +
  stat_function(fun = dnorm) + 
    stat_function(fun = dnorm, 
                xlim = c(2,3),
                geom = "area",
                fill="green")+
  labs(
    title = "Distribution of weights of students",
    x="",
    y=""
  ) +
  geom_segment(x=0, xend=0, y=0, yend=0.4, linetype="dashed") +
  annotate("text", x=2, y=0.07, label="lower limit")+
  annotate("text", x=0.2, y=0.1, label="mean=50")+
theme_classic() +
  theme(axis.text.x = element_blank(),
        axis.text.y = element_blank()
        ) 

हम निचली सीमा ज्ञात करने में रुचि रखते हैं, जो कि ८५% (१-१५%) है। इसलिए, हम इस बिंदु पर मूल्य खोजने में रुचि रखते हैं। ऐसा करने के लिए हम ‘qnorm’ फ़ंक्शन का उपयोग कर सकते हैं।

qnorm(0.85, 50, 5)

## [1] 55.18217

दो संबंधित वीडियो इस प्रकार हैं।