डेटा को सारांशित करने के और तरीके
स्थान
अक्सर, डेटा की विशेषताओं को व्यक्त करने के लिए प्लॉट प्रदर्शित करना संभव नहीं है। ऐसे मामलों में हमें संक्षेप करने के लिए कुछ अन्य तरीकों की आवश्यकता होती है। यदि आप हमारे पिछले लेख से याद करते हैं, तो हिस्टोग्राम अधिकतर होते हैं यह समझने के लिए कि कितने में, न्यूनतम, अधिकतम, `अधिकांश डेटा में हो रहा है’ या ‘कितने कम या इससे ज़्यादा’ हैं। उदाहरण के लिए क्या अधिकांश छात्रों का वजन 60 किलो से कम होता है?
प्लॉटिंग के बिना, इनमें से कुछ जानकारी को अन्य गैर-ग्राफिक माध्यमों से संप्रेषित किया जा सकता है। ये स्थान और आकार हैं।
केंद्र स्थान
शायद सबसे व्यापक रूप से इस्तेमाल किया जाने वाला केंद्रीय स्थान औसत है। यदि आपके पास 1000 छात्रों के वजन का डेटा है और आप इन सभी भारों को एक संख्या के रूप में बताना चाहते हैं, तो केंद्रीय स्थान एक उपाय है। इसलिए, जब हम नमूना या जनसंख्या पैरामीटर (उदाहरण के लिए 1000 छात्रों के वजन) की वर्णना करने के लिए एक संख्या या मान का उपयोग करते हैं तो हम केंद्रीय स्थान का उपयोग करते हैं।
सबसे व्यापक रूप से इस्तेमाल किया जाने वाला केंद्रीय स्थान औसत या माध्य है। माध्य की गणना करने के लिए, सभी मानों को जोड़ा जाता है और फिर जितनी संख्यायों (या मानों )को जोड़ा गया’, उस संख्या से विभाजित किया जाता है।
\[ \mu =\frac{\sum_{i = 1}^{n}{(x_i)}}{n} \] जहाँ \(\mu\)मतलब औसत \(x_i\) हैं संख्याएं या मानें \(n\) मानों की संख्या
यानी यदि 10 संख्याएं 1,2,3,2,5,4,3,6,5, और 6 हैं, तो उनका औसत है
\[ \frac{(1+2+3+2+5+4+3+6+5+6)}{10} = 3.7 \]
R में, इसकी गणना करने के लिए mean नामक एक फलन(function) है। उपरोक्त संख्याओं के माध्य (mean) की गणना के लिए कोड नीचे दिखाया गया है।
mean(c(1,2,3,2,5,4,3,6,5,6))## [1] 3.7यदि हम एक और संख्या या कुछ संख्याएँ जोड़ते हैं जो श्रृंखला में मौजूदा संख्याओं से बहुत दूर नहीं हैं, तो नए औसत के रूप में हमें मागभग एक समान संख्या प्राप्त होगी। नीचे, मैंने तीन और संख्याएँ जोड़ी हैं, २,४ और ७।
mean(c(1,2,3,2,5,4,3,6,5,6,2,4,7))## [1] 3.846154नया औसत या माध्य पहले परिकलित औसत से बहुत दूर नहीं है।
हालाँकि, यदि हम एक ऐसी संख्या जोड़ते हैं जो श्रृंखला में मौजूदा संख्याओं से कुछ दूर है, तो चीजें बदल सकती हैं।
mean(c(1,2,3,2,5,4,3,6,5,6,12))## [1] 4.454545इस बार हमने एक नंबर (12) जोड़ा और औसत ४.४५ हो गया। तो, केवल एक उच्च मूल्य या कम मूल्य की उपस्थिति औसत को खराब कर सकती है । यह बहुत बार हो सकता है और इसलिए, औसत बहुत मजबूत नहीं है। और औसत का उपयोग करते समय हमेशा सावधानी बरतनी चाहिए।
एक अन्य केंद्रीय स्थान माप, जो औसत से अधिक मजबूत है, median है। यदि और जब संख्याओं को आप छोटे से बड़े में सजाते(क्रमबद्ध) हैं तो सबसे बीच में संख्या median है ।
यदि प्रेक्षणों की विषम संख्या है, तो यह होता है
\[ median(x)=x_{(n+1)/2} \]
तो अगर 5 संख्याएं 1,2,3,2 और 5 हैं, तो हम उन्हें छोटे से बड़े में सजाते हैं। यह 1,2,2,3,5 हो जाता है। 5 अंक हैं। तो n=5 और n+1=6। (n+1)/2=3. अतः median तीसरी संख्या है।
यदि प्रेक्षणों की संख्या सम हो, तो यह है
\[ median(x)=\frac{x_{n/2}+x_{(n/2)+1}}{2} \]
इसलिए, अगर हमारे पास 6 नंबर 1,2,3,2,5 और 4 हैं, तो हम पहले उन्हें छोटे से बड़े में सजाते हैं। यह 1,2,2,3,4,5 हो जाता है। 6 अंक हैं। तो, एन = 6। n/2=3 और (n/2)+1=4. तीसरी और चौथी संख्या 2 और 3 हैं। अतः, मीडियन (2+3)/2=2.5 है।
R में, इनकी गणना करने के लिए median नामक एक function है।
median(c(1,2,3,2,5,4))## [1] 2.5क्या होगा यदि वेरिएबल संख्यात्मक नहीं है? हम केंद्रीय स्थान को कैसे मापेंगे? उस समय हम ‘मोड’ का उपयोग करके हैं। जो सबसे अधिक बार होने वाले अवलोकन को परिभाषित करता है। यह संख्यात्मक वेरिएबल के लिए भी मान्य है। हम किसी संख्या की उपस्थिति (कितनी बार या कितनी संख्या) को माप सकते हैं। या, हम डिब्बे (bins) बना सकते हैं (उदाहरण के लिए, 1-5, 6-10 इत्यादि) और उपस्थिति को माप सकते हैं।
यदि हमारे पास संख्या 1,2,3,2,5 और 4 है, तो 2 सबसे अधिक बार आता है। अतः बहुलक (mode) 2 है। यदि हमारे पास a,b,c,a,c,a,b और a मान हैं, तो बहुलक a है क्योंकि यह सबसे अधिक बार आता है। एक नमूने में एक से अधिक मोड हो सकते हैं।
R में मोड की गणना करने के लिए कोई इनबिल्ट फ़ंक्शन नहीं है। हालांकि, आप अपना खुद का लिख सकते हैं।
mode.cal <- function(x) {
unique.x <- unique(x)
unique.x[which.max(tabulate(match(x, unique.x)))]
}
mode.cal(c(1,2,3,2,5,4))## [1] 2केंद्रीय स्थान के दो अन्य उपाय अक्सर उपयोग किए जाते हैं। ज्यामितीय माध्य (Geometric Mean) का उपयोग वृद्धि (Growth) की केंद्रीय स्थिति को समझने के लिए किया जाता है। उदाहरण के लिए, यदि किसी शेयर की कीमत में लगातार तीन महीनों में 1%, 1.5%, 4% की वृद्धि हुई है, तो औसत वृद्धि की गणना ज्यामितीय माध्य से की जाती है।
\[ GM=\sqrt[n]{x_1\times x_2\times x_3 ... x_n} \]
दूसरा भारित माध्य (Weighted mean ) है जिसका उपयोग तब किया जाता है जब विभिन्न अवलोकनों के अलग-अलग भार होते हैं। उदाहरण के लिए, किसी को 10 घंटे के लिए काम पर रखने की लागत 100 है। उसी व्यक्ति को 6 घंटे के लिए काम पर रखने की लागत 80 है और 2 घंटे के लिए 20 है। तब प्रति घंटे की औसत लागत की गणना के लिए हम weighted mean का इस्तेमाल करते हैं |
\[ \frac {{100 \times 10} + {80 \times 6} + { 20 \times 2}}{10+6+2} \]
सूत्र है
\[ {Weighted} \space {\bar x} = \frac {\sum{f_i \times x_i}}{\sum f_i} \]
ज्यामितीय माध्य की गणना R में इस प्रकार की जाती है
# growth of 1% means new value is 1.01 (i.e. 1 + 1%)
x<-c(1.01,1.015,1.04) # Stock price increased 1%, 1.5% and 4%
exp(mean(log(x)))## [1] 1.021583भारित माध्य की गणना weighted.mean फ़ंक्शन का उपयोग करके R में की जाती है। इनपुट के रूप में दो वैक्टर दिए जाते हैं। पहला मान है और दूसरा वजन है।
cost<-c(550,420,800)
hour<-c(8,6,2)
weighted.mean(cost, hour) ## [1] 532.5गैर-केंद्रीय स्थान
केंद्रीय स्थान मानों की वर्णना करते हैं। हालांकि, वितरण के गुणों को समझने के लिए भी आपको अक्सर आवश्यकता होती है। यदि औसत एक केंद्रीय संख्या प्रदान करता है, तो हम उससे अधिक जानना चाह सकते हैं। वह मान क्या है जिसके नीचे सबसे कम 25% प्रेक्षण हैं, इत्यादि । हम ऐसे मामले में चतुर्थक (Quartiles ) और प्रतिशतक (Percentile ) का उपयोग करते हैं। चतुर्थक वे उपाय या मान हैं जो एक क्रमबद्ध डेटा को चार बराबर भागों में विभाजित करते हैं (प्रेक्षणों की संख्या के आधार पर)।
25% प्रेक्षण न्यूनतम मान और प्रथम चतुर्थक (Q1) के बीच होते हैं, अगले 25% Q1 और Q2 के बीच होते हैं और इसी तरह आगे भी। Q2 बीच की प्रेक्षण को परिभाषित करता है, या 50% पर्सेंटाइल। अत: यह माध्यिका (Median ) है।
Quartiles
चतुर्थक की गणना quantile फ़ंक्शन का उपयोग करके R में की जा सकती है। यह मानों के वेक्टर को पहले पैरामीटर के रूप में लेता है। फिर, इसे पैरामीटर probs की आवश्यकता होती है जहां आप प्रतिशतक निर्दिष्ट कर सकते हैं। Q1 के लिए, आप 0.25 (25%) दर्ज कर सकते हैं। आप विभिन्न शतमक का सदिश प्रदान कर सकते हैं। उदाहरण के लिए c(0.25,0.5,0.75)।
quantile(c(1,2,3,4,5,6), c(0.25,0.5,0.75))## 25% 50% 75%
## 2.25 3.50 4.75आप इसका उपयोग करके किसी भी शतमक (0 से 100) में निहित मानों का पता लगा सकते हैं। 25 वाँ प्रतिशतक Q1 है, 50 वाँ Q2 उत्तर है।
फैलाव
फैलाव इंगित करता है कि अवलोकन किस हद तक बिखरे हुए हैं। यह केंद्रीय स्थान माप में हमारे विश्वास को प्रभावित करता है। यदि अवलोकन के एक सेट का औसत 20 है और अवलोकनों की सीमा 19 और 21 के बीच है (सभी अवलोकन 19 और 21 के बीच हैं), तो हम औसत द्वारा अवलोकन के सेट की वर्णना पर बहुत आश्वस्त हो सकते हैं। हालाँकि, यदि सीमा -20 से 100 तक है, तो आत्मविश्वास कम हो जाता है।
सीमा (Range ) न्यूनतम और अधिकतम मान (दोनों सम्मिलित) को इंगित करता है जिसके बीच प्रेक्षण के सभी मान निहित होते हैं। हम इसकी गणना करने के लिए R में range फ़ंक्शन का उपयोग कर सकते हैं।
range(c(1,2,3,4,3,5,3,6))## [1] 1 6वरियन्स (Variance) माध्य (mean ) से प्रेक्षणों (observation ) की दूरी (वर्ग) को इंगित करता है। यह प्रेक्षणों और माध्य के अंतर के वर्ग का औसत है।
\[ s^2 = \frac {\sum (x_i - \bar {x} )^2}{n-1} \] \(s^2\) वरियन्स है \(\bar x\) औसत है \(n\) अवलोकन की संख्या है
ऋणात्मक संख्या (negative number) से बचने के लिए वर्ग का उपयोग किया जाता है। जब हम इस संख्या या वरियन्स का वर्गमूल लेते हैं, तो हमें स्टैण्डर्ड डेविएशन (Standard Deviation ) प्राप्त होता है।
R में, वरियन्स की गणना var फ़ंक्शन का उपयोग करके की जाती है और स्टैंडर्ड डेविएशन की गणना sd फ़ंक्शन का उपयोग करके की जाती है।
अब मान लीजिए कि आपके पास दो नमूने (सैंपल ) हैं और आप यह समझना चाहते हैं कि किसका variance अधिक है। एक नमूना meter में है और दूसरा centimeter में है। एक मजबूत उदाहरण बनाने के लिए, आइए हम समान मान लें। हमारे पास centimeter में एक नमूना है। हम इन्ही सेंटीमीटर के मानों को मीटर में परिवर्तित करके एक और नमूना लेते हैं।
in.cm<-c(100,200,300,400)
in.m<-c(1,2,3,4)
c(sd.cm=sd(in.cm), sd.m=sd(in.m))## sd.cm sd.m
## 129.099445 1.290994दिलचस्प! इकाइयों में अंतर के कारण समान मान के स्ट्रैंडर्ड डेविएशन बदल जाते हैं। अगर नमूनों की संख्या कम है या इकतियों का परिवर्तन संभव है तो यह इतनी बड़ी समस्या नहीं है । लेकिन गैर परिवर्तनीय इकाइयों (उदाहरण के लिए किग्रा (kg ), मी(m ) आदि) के साथ यह एक मुद्दा बन सकता है। ऐसे नमूनों के प्रसरण(variance ) की तुलना करने के लिए, हम प्रसरण के गुणांक (coefficient of variance ) का उपयोग करते हैं। यह प्रतिशत में दिया जाता है और स्टैण्डर्ड डेविएशन को औसत से विभाजित करके परिकलित किया जाता है।
आइए हम उपरोक्त उदाहरण से गणना करें।
c(cov.cm=sd(in.cm)/mean(in.cm), cov.m=sd(in.m)/mean(in.m))## cov.cm cov.m
## 0.5163978 0.5163978दोनों में विचरण का एक ही गुणांक है!
तिरछापन
विषमता संख्यात्मक unimodal 1 वेरिएबल के वितरण के आकार को इंगित करती है। नीचे दी गई छवि में तीन प्रकारों का वर्णन किया गया है।
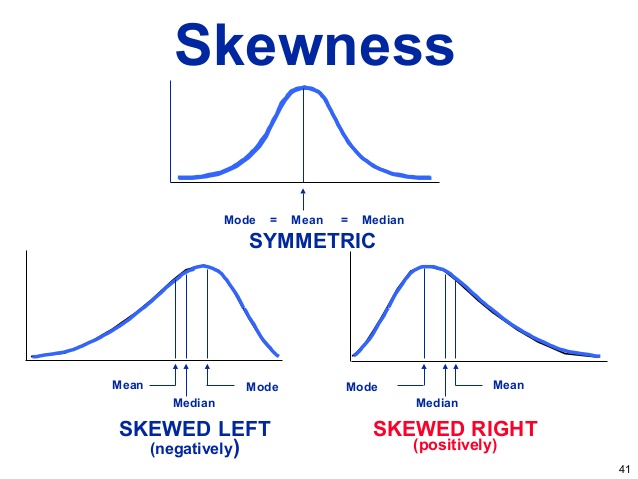
क्रेडिट: डगलस कॉलेज लर्निंग सेंटर
माध्य (Mean ), माध्यिका (Median ) और बहुलक (Mode ) की गणना करके और तुलना करने या प्लॉट करने के अलावा, पियर्सन के तिरछापन गुणांक (Pearson’s skewness coefficient ) का उपयोग करके तिरछापन की गणना हो सकती है है। इसकी गणना R में moments लाइब्रेरी से फंक्शन skewness का उपयोग करके की जा सकती है।
moments::skewness(rnorm(100))## [1] 0.2709473जब पियर्सन का तिरछापन गुणांक 0 के बराबर या लगभग बराबर होता है, तो वितरण सममित (Symmetric) होता है। 0 से कम होने पर यह ऋणात्मक (Negatively Skewed) रूप से सममित होता है। और जब 0 से अधिक होता है, तो यह धनात्मक (Positively Skewed) रूप से सममित होता है।
संबंधित वीडियो नीचे संलग्न है।
Footnote
यूनिमोडल का अर्थ है एक मोड होना↩︎