সম্ভাবনা বিতরণ
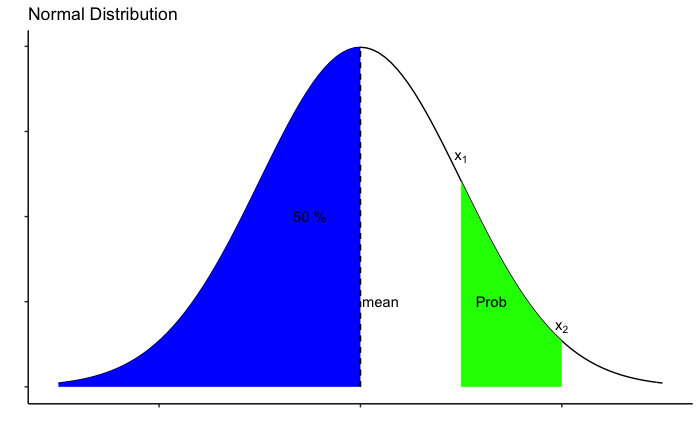
সম্ভাবনা বিতরণ
আমাদের শেষ নিবন্ধে আমরা সম্ভাবনার মূল বিষয়গুলি র ব্যাপারে আলোচনা করেছিলাম এবং দেখেছিলাম কীভাবে এটি অনুভূতিগতভাবে গণনা করা হয় । এই নিবন্ধে আমরা কীভাবে গাণিতিক ফাংশন থেকে সম্ভাবনাগুলি গণনা করা যায় তা বোঝার চেষ্টা করব। কিছু নির্দিষ্ট ফাংশন রয়েছে যা দিয়ে গণিতবিদদের দ্বারা প্রতিষ্ঠিত কিছু সূত্র ব্যবহার করে সম্ভাবনাগুলি গণনা করা যায়। বাস্তব জীবনে, বেশ কয়েকটি রান্ডম ভ্যারিয়েবল (যেমন পূর্ববর্তী নিবন্ধগুলির শিক্ষার্থীদের ওজন) এই ফাংশনগুলির একটি সম্ভাব্যতার নিদর্শন অনুসরণ করে বা অনুমান করা হয় যে করে। এই জাতীয় ক্ষেত্রে, সম্ভাবনাগুলি গণিত হিসাবে গণনা করা যেতে পারে। এই ফাংশনগুলি আমাদের সমস্ত সম্ভাব্য ফলাফল এবং তাদের সম্পর্কিত সম্ভাব্যতা সরবরাহ করে। এবং এটিকে সম্ভাব্যতা বন্টন বলা হয়।
সম্ভাব্যতা বিতরণ ফাংশন দুটি ধরণের হয়। একটি যেখানে ভেরিয়েবলগুলি পৃথক এবং অন্য যেখানে ভেরিয়েবলগুলি অবিচ্ছিন্ন। এই নিবন্ধে, আমরা সংক্ষেপে কিছু ব্যবহৃত ফাংশন নিয়ে আলোচনা করব।
পৃথক সম্ভাবনা বন্টন
দ্বিপদী সম্ভাব্য বন্টন
একটি রান্ডম ভেরিয়েবল দ্বিপদী বিতরণ অনুসরণ করে যদি
- রান্ডম ভেরিয়েবল টি বিযুক্ত (ডিসক্রিট ) ২. রান্ডম ভেরিয়েবল টি নির্দিষ্ট সংখ্যক বার পরিলক্ষিত হয় (একটি মুদ্রা টসিং এবং ফলাফল পর্যবেক্ষণের কল্পনা করুন) ৩. সম্ভাব্য দুটি ফলাফলই রয়েছে। তাদের কে 0 বা 1 হিসাবে, সাফল্য বা ব্যর্থতা বা সত্য বা মিথ্যা হিসাবে লেবেল করা যেতে পারে ৪. প্রতিটি ফলাফলের সাথে যুক্ত সম্ভাবনা রয়েছে যা যোগ যোগ করলে ১ হয় । সাফল্যের সম্ভাবনা যদি p হয় তবে ব্যর্থতার সম্ভাবনা (1-p ) হবে। ৫. প্রতিটি ফলাফল অপরটির থেকে স্বাধীন।
n টি রান্ডম নির্বাচন থেকে y সাফল্যের সম্ভাবনা হলো
যেখানে y হ’ল সাফল্যের সংখ্যা, p হ’ল সাফল্যের সম্ভাবনা এবং n হ’ল নমুনার সংখ্যা।
R এ , dbinom ফাংশন ব্যবহার করে এর সম্ভাব্যতা গণনা করতে পারে।
মনে করুন যে আপনি জানেন যে মেসি পেনাল্টি শ্যুটআউটে 77% বার গোল করে। এবার , আপনি বুঝতে চান যে মেসি যদি 5 টি পেনাল্টি কিক নেন, তবে তাদের মধ্যে তিনটি গোল হওয়ার সম্ভাবনা কতটা।
dbinom(3,5,0.77)## [1] 0.241506যদি আমাদের ৩ টির বেশি গোল না হওয়ার সম্ভাবনার কথা জিজ্ঞেস করা হয়, তখন ? এটি করার দুটি উপায় আছে। প্রথম উপায়ে, আমরা 0,1,2 এবং 3 টি গোল এর সম্ভাবনার যোগ করি।
sum(dbinom(0:3,5,0.77))## [1] 0.3250616দ্বিতীয়টিতে, আমরা আরেকটি ফাংশন pbinom ব্যবহার করি।
pbinom(3,5,0.77)## [1] 0.3250616বিতরণের গড়টি সম্ভাব্যতা আর নমুনা আকারের (সংখ্যা ) গুণ। আমাদের উদাহরণস্বরূপ, আমরা 5 কিকের মধ্যে গড় 5 * 0.77 ( 3.85) গোল আশা করতে পারি। স্ট্যান্ডার্ড ডেভিয়েশন হলো .
পয়সন সম্ভাব্যতা বিতরণ
যখনই আমরা একটি বিরতিতে, ভ্যারিয়েবল এর এক নির্দিষ্ট ফলাফলের সংখ্যার ব্যাপারে কথা বলি, যার গড় আমাদের জানা, তখন আমরা পয়েশন ব্যবহার করি। উদাহরণস্বরূপ, প্রতিদিন কোনও দোকানে আগত গ্রাহকদের সংখ্যা বা এক মাসে মেসির দ্বারা গোল এর সংখ্যা। বিরতিটি সময়, স্থান বা ভলিউম হতে পারে। উদাহরণস্বরূপ, একটি পুকুর থেকে প্রতি লিটার পানিতে জীবের সংখ্যা।
একটি বিরতিতে y ইভেন্টগুলির বা কোনও নির্দিষ্ট ফলাফলের পর্যবেক্ষণের সম্ভাবনা দেওয়া হয়
যেখানে a হ’ল ব্যবধানে নির্দিষ্ট ফলাফলের গড় সংখ্যা।
দ্বিপদী ফাংশনের অনুরূপ, R এ পায়সনের জন্যও ফাংশন রয়েছে ।
ধরে নিই যে মেসি গড়ে প্রতি 1 ম্যাচে 2 টি স্কোর করে, আমরা গণনা করতে চাই যে পরের 1 ম্যাচে মেসির 2 টি গোল করার সম্ভাবনা কত।
dpois(1,2)## [1] 0.2706706আমরা যদি কমপক্ষে একটি গোল এর সম্ভাবনা জানতে চাই তবে দুটি উপায় আছে। আমরা 0 এবং 1 গোলের সম্ভাব্যতাগুলি যুক্ত করতে পারি বা ppois ফাংশন ব্যবহার করতে পারি।
sum(dpois(0:1,2))## [1] 0.4060058ppois(1,2)## [1] 0.4060058বিতরণের গড় হলো a যেটা আমাদের জানা । স্ট্যান্ডার্ড ডেভিয়েশন হ’ল
অবিচ্ছিন্ন সম্ভাবনা ফাংশন
অবিচ্ছিন্ন সম্ভাবনার ফাংশন অবিচ্ছিন্ন ভেরিয়েবলের সম্ভাব্যতা সরবরাহ করে। সর্বাধিক ব্যবহৃত অবিচ্ছন্ন সম্ভাব্যতা বিতরণ ফাংশন হ’ল সাধারণ/স্বাভাবিক (নরমাল) বিতরণ।
সাধারণ সম্ভাবনা বন্টন
সাধারণ সম্ভাবনা বিতরণ আছে
- বেল আকারের বক্ররেখা
- গড় (যা কেন্দ্রীয় মান) সম্পর্কে প্রতিসম
- লেজগুলি যা কখনও x অক্ষকে (এক্সিস) স্পর্শ করে না (অ্যাসিপটোটিক)
- বিতরণ দুটি পরামিতি, গড় এবং মান বিচ্যুতি (স্ট্যান্ডার্ড ডেভিয়েশন) দ্বারা বর্ণনা করা যেতে পারে
- বক্ররেখার নিচে মোট ক্ষেত্রফল 1 এবং
- একটি বিরতির সম্ভাবনা হ’ল অন্তরালের পরিধিটির বক্ররেখার ক্ষেত্রফল
library(ggplot2)
ggplot(data.frame(x = c(-3, 3)), aes(x)) +
stat_function(fun = dnorm) +
stat_function(fun = dnorm,
xlim = c(-3,0),
geom = "area",
fill="blue") +
stat_function(fun = dnorm,
xlim = c(1,2),
geom = "area",
fill="green")+
labs(
title = "(Standard)Normal Distribution",
x="",
y=""
) +
geom_segment(x=0, xend=0, y=0, yend=0.4, linetype="dashed") +
annotate("text", x=1, y=0.27, label=expression(x[1]))+
annotate("text", x=2, y=0.07, label=expression(x[2]))+
annotate("text", x=1.3, y=0.1, label="Prob")+
annotate("text", x=0.2, y=0.1, label="mean=0")+
annotate("text", x=-0.5, y=0.2, label="50 %")+
theme_classic() +
theme(axis.text.x = element_blank(),
axis.text.y = element_blank()
) 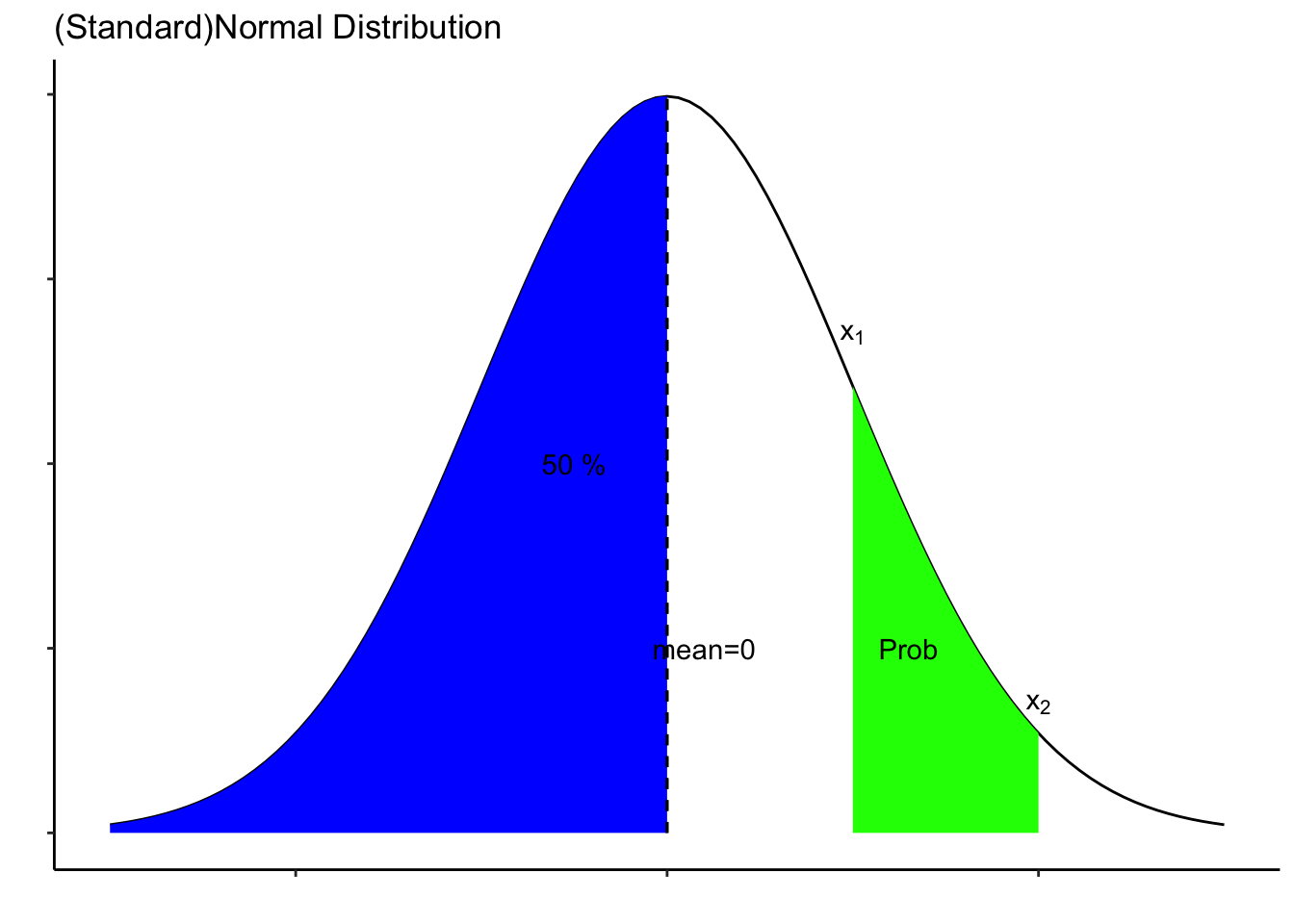
স্ট্যান্ডার্ড স্বাভাবিক (Standard Normal) বিচ্যুতির সম্ভাবনাগুলি z-table নামে একটি সারণীতে পাওয়া যায়। যেহেতু টেবিলটি স্ট্যান্ডার্ড এর সম্ভাব্যতা সরবরাহ করে, তাই আমরা রান্ডম ভ্যারিয়েবল (x) কে z-value -তে রূপান্তর করি ।
z-value মূলত x অক্ষে ভেরিয়েবলের নির্দিষ্ট মানের অবস্থান নির্দেশ করে (গড় থেকে কত দূরে)।
R -এ, z-table ব্যবহার করার দরকার নেই। binomial এবং Poisson এর ক্ষেত্রে যেমন ফাঙ্কশন রয়েছে, Normal Distribution এর জন্য ও ফাঙ্কশন রয়েছে ।
ধরা যাক একটি শ্রেণীর শিক্ষার্থীদের ওজনের গড় হার ৫০ এবং স্ট্যান্ডার্ড ডেভিয়েশন ৫ রয়েছে। আমরা ক্লাসের শীর্ষ 15% ওজনের নিম্ন সীমাটি জানতে চাই।
ggplot(data.frame(x = c(-3, 3)), aes(x)) +
stat_function(fun = dnorm) +
stat_function(fun = dnorm,
xlim = c(2,3),
geom = "area",
fill="green")+
labs(
title = "Distribution of weights of students",
x="",
y=""
) +
geom_segment(x=0, xend=0, y=0, yend=0.4, linetype="dashed") +
annotate("text", x=2, y=0.07, label="lower limit")+
annotate("text", x=0.2, y=0.1, label="mean=50")+
theme_classic() +
theme(axis.text.x = element_blank(),
axis.text.y = element_blank()
) 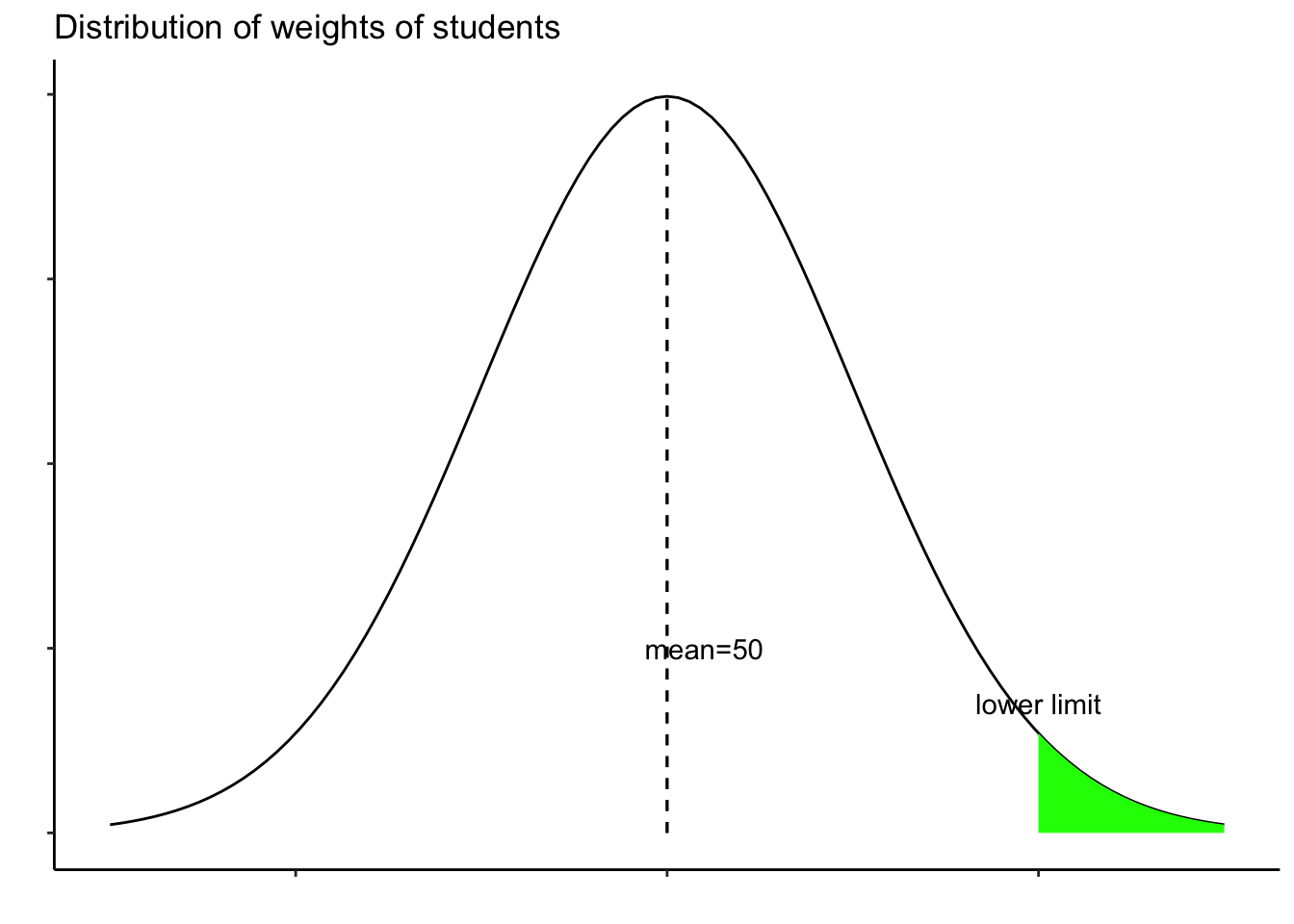
আমরা নিম্ন সীমাটি সন্ধান করতে আগ্রহী, যা 85% (1- 15%)। সুতরাং, আমরা এই পয়েন্ট এ (৮৫%) মান সন্ধান করতে আগ্রহী। আমরা এটি করতে qnorm ফাংশনটি ব্যবহার করতে পারি।
qnorm(0.85, 50, 5)## [1] 55.18217দুটি সম্পর্কিত ভিডিও নিচে দেয়া হলো ।