নমুনা ও নমুনা বিতরণ
নমুনা
একটি নমুনা একটি জনসংখ্যার একটি উপসেট। বেশিরভাগ সময় জনসংখ্যার ডেটা সংগ্রহ করা খুব ব্যয়বহুল বা অসম্ভব। অনুমানের পরিসংখ্যানের সম্পূর্ণ ধারণা (যা পরবর্তীকালে মেশিন লার্নিং এবং এআইতে বিকশিত হয়েছে) নমুনার পরামিতিগুলি অধ্যয়ন করে জনসংখ্যার পরামিতিগুলির অনুমানের চারপাশে ঘোরে। নমুনা এবং নমুনা বিতরণ হ’ল চারটি চাকাগুলির মধ্যে দুটি যার উপর অনুমানমূলক পরিসংখ্যান (এবং মেশিন লার্নিং এবং এআই) চলে। অন্য দুটি হ’ল [বর্ণনামূলক পরিসংখ্যান] (https://www.eds.ninja/bn/post/%E0%A6%A1%E0%A7%87%E0%A6%9F%E0%A6%BE-%E0%A6%B8%E0%A6%82%E0%A6%95%E0%A7%8D%E0%A6%B7%E0%A6%BF%E0%A6%AA%E0%A7%8D%E0%A6%A4-%E0%A6%95%E0%A6%B0%E0%A6%BE%E0%A6%B0-%E0%A6%86%E0%A6%B0%E0%A6%93-%E0%A6%89%E0%A6%AA%E0%A6%BE%E0%A6%AF%E0%A6%BC/) এবং [সম্ভাব্যতা] (https://www.eds.ninja/bn/post/%E0%A6%B8%E0%A6%AE%E0%A7%8D%E0%A6%AD%E0%A6%BE%E0%A6%AC%E0%A6%A8%E0%A6%BE-%E0%A6%A4%E0%A6%A4%E0%A7%8D%E0%A6%AC-%E0%A6%8F%E0%A6%B0-%E0%A6%AE%E0%A7%82%E0%A6%B2/) যা আমরা ইতিমধ্যে কভার করেছি।
একটি বিশ্লেষণ ভালো বা দৃঢ হতে গেলে নমুনা টি জনসংখ্যার প্রতিরূপ হতে হবে । নমুনা দুটি ধরণের মধ্যে বিভক্ত করা যেতে পারে; রান্ডম এবং নন -রান্ডম। নন র্যান্ডম স্যাম্পলিংয়ের অর্থ হল যে নমুনাগুলি এলোমেলোভাবে (রান্ডমলি) নির্বাচন করা হয়নি। এলোমেলোভাবে নির্বাচিত নয় এমন নমুনাগুলি আনুপাতিক পরিসংখ্যান বিশ্লেষণের জন্য উপযুক্ত নয় এবং আমরা সেগুলিতে মনোনিবেশ করব না।
এলোমেলোভাবে (রান্ডমলি) নির্বাচিত নমুনাগুলি পরিসংখ্যান বিশ্লেষণের জন্য উপযুক্ত। নির্বাচনটি নিখুঁতভাবে রান্ডম । মনে করুন আপনি ভারতীয় জনসংখ্যার সাথে সম্পর্কিত কিছু পরামিতি বুঝতে চান। বিশ্লেষণ চালাতে আপনি রান্ডমলি কিছু ভারতীয় নাগরিক নির্বাচন করতে পারেন। এটি লটারির মতো বা একটি টুপি থেকে সংখ্যা বাছাইয়ের মতো। এটিকে সাধারণ র্যান্ডম নমুনা বলা হয়।
স্যাম্পলিংয়ের আরেকটি উপায় হ’ল নমুনা ফ্রেমটিকে ব্লক এ বিভক্ত করা যেতে পারে। শেষ উদাহরণটি ব্যবহার করে, আপনি প্রথমে রান্ডমলি x সংখ্যক লোক নির্বাচন করতে পারেন। এরপরে আপনি এগুলিকে কিছু দলে ভাগ করতে পারেন। তারপরে কেবল প্রথম গ্রুপ থেকে রান্ডমলি একজনকে নির্বাচন করুন। যদি সেই ব্যক্তি নমুনায় নবম হন, আপনি প্রতিটি গ্রুপ থেকে নবম নির্বাচন করা চালিয়ে যান। একে পদ্ধতিগত র্যান্ডম নমুনা বলা হয়
বিবেচিত প্যারামিটারের ক্ষেত্রে জনসংখ্যাকে যখন heterogeneous হিসাবে বিবেচনা করা হয় তখন স্ট্র্যাটেড রান্ডম নমুনা ব্যবহার করা হয়। কিছু গ্রুপ তৈরি করা হয় যেখানে প্রতিটি গ্রুপ heterogeneous|(বিষম ) উদাহরণস্বরূপ, যদি আমরা ফুটবল খেলোয়াড়দের দ্বারা প্রতি ম্যাচে করা গোলগুলি বিশ্লেষণ করতে চাই, আমরা তাদের যে স্তরটিতে খেলে বা তারা যে পজিশনে খেলে তাতে ভাগ করে নিতে পারি। কারণ একজন গোলরক্ষক এবং একজন স্ট্রাইকারের দ্বারা করা গোলগুলির তুলনাটি বোধগম্য নয়।
ক্লাস্টার রান্ডম নমুনা, যখন লক্ষ্য গোষ্ঠীগুলি প্রাকৃতিক ভাবে দল গঠন করে, তখন ব্যবহৃত হয়। উদাহরণস্বরূপ, আপনি যদি মার্কিন যুক্তরাষ্ট্রে অটোমোবাইল উত্পাদনকারীদের মধ্যে লিঙ্গ বৈচিত্র্য বিশ্লেষণ করতে চান তবে আপনি প্রথমে রান্ডমলি কয়েকটি সংস্থা নির্বাচন করতে পারেন। এবং তারপরে সেই সংস্থাগুলিতে পরামিতিগুলি পরিমাপ করতে পারেন।
** অ-সম্ভাব্য নমুনা কেবল অনুসন্ধান বিশ্লেষণের জন্য উপযুক্ত। সম্ভাব্য নমুনা সন্ধান এবং অনুসন্ধান উভয় ক্ষেত্রেই উপযুক্ত।
নমুনা বিতরণ
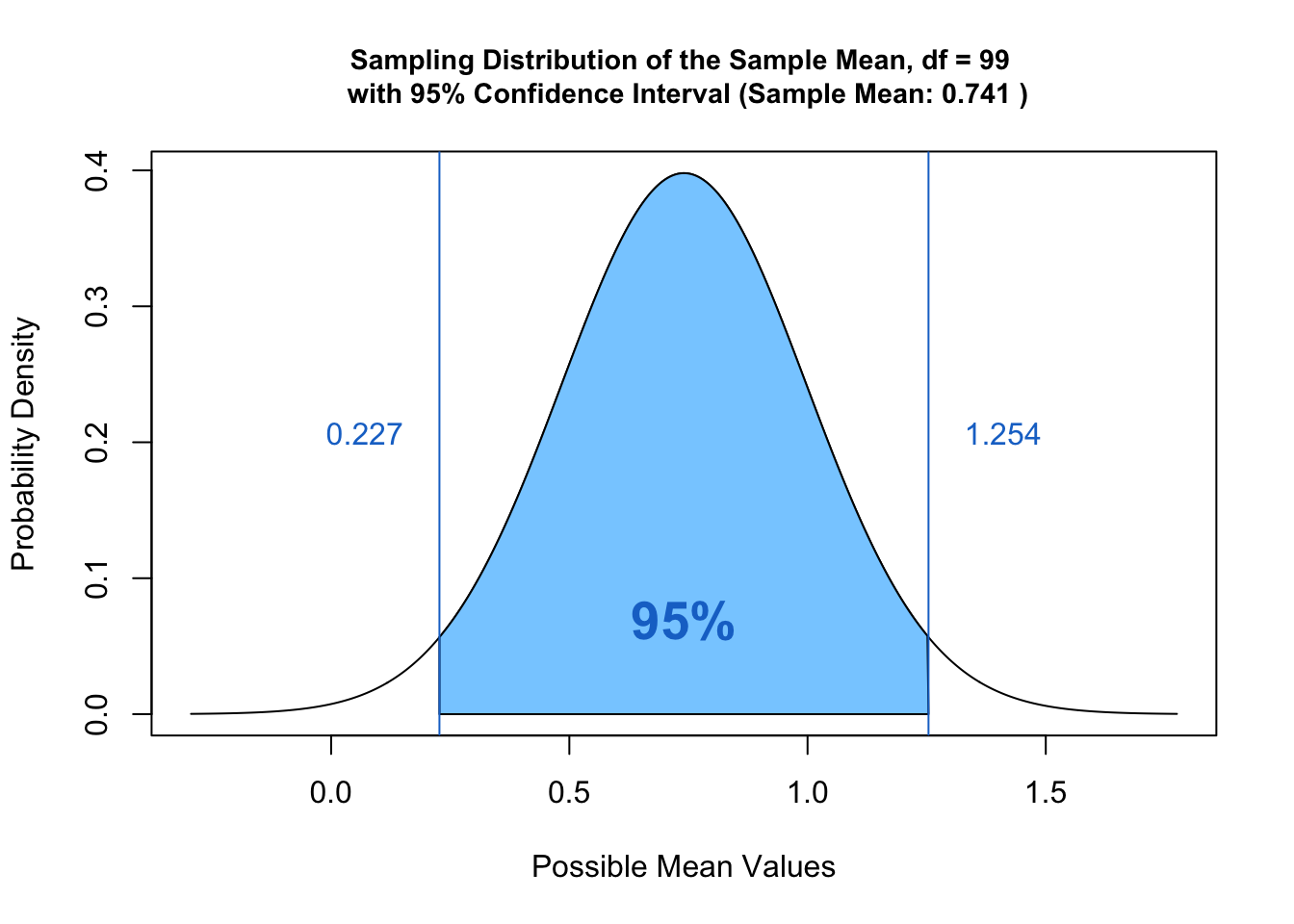
যখন আমরা জনসংখ্যার একই পরামিতিটি অনুমানের লক্ষ্য নিয়ে কোনও নমুনার প্যারামিটার পরিমাপ করি তখন প্রাকৃতিকভাবে উত্থাপিত প্রশ্নগুলির মধ্যে একটি হল যথার্থতার প্রশ্ন। উদাহরণস্বরূপ, আসুন আমরা ধরে নিই যে আমরা একটি বিদ্যালয়ের সমস্ত শিক্ষার্থীর গড় ওজন পরিমাপ করব এবং এটি গণনা করার জন্য আমরা একটি নমুনা নিয়েছি। যদি নমুনা গড় ওজন x হয়, তবে জনগণের গড় ওজন (সমস্ত শিক্ষার্থী) এটি (x) কতটা সঠিকভাবে প্রতিফলিত করে, সেটা প্রশ্ন। বা, আমরা এটি সম্পর্কে কতটা আত্মবিশ্বাসী বা, জনসংখ্যার পরামিতি থেকে এটি কতটা দূরে। নমুনা বিতরণ আমাদের এই প্রশ্নের উত্তর দিতে সহায়তা করে। এটি নমুনা পরিসংখ্যান এবং জনসংখ্যার পরিসংখ্যানের মধ্যে সম্পর্ককে দেখায়।
নিম্নলিখিতটি সাধারণ বন্টনের জন্য কেন্দ্রীয় প্রবণতা ব্যবস্থা (একক গড়, একক অনুপাত, গড়ের মধ্যে পার্থক্য এবং অনুপাতের মধ্যে পার্থক্য) জন্য প্রতিষ্ঠিত এবং বিবেচিত।
- সমস্ত নমুনা প্যারামিটার 68.3% সময় একটি স্ট্যান্ডার্ড ত্রুটির (নমুনার মানক বিচ্যুতি) মধ্যে থাকবে
- 95.5% সময়ের মধ্যে এটি দুটি স্ট্যান্ডার্ড ত্রুটি এর মধ্যে থাকবে এবং ৩. 99.7% সময় এটি তিনটি স্ট্যান্ডার্ড ত্রুটির মধ্যে থাকবে
সঠিক সম্ভাবনাটি z-stat ব্যবহার করে গণনা করা হয়, যা জনসংখ্যার সম্ভাব্য সমস্ত প্যারামিটার এর (একই জনগোষ্ঠীর বিভিন্ন নমুনা থেকে) বিতরণে নমুনা প্যারামিটারএর অবস্থান নির্দিষ্ট করে।
z-stat প্রতিটি কেন্দ্রীয় প্রবণতার জন্য বিভিন্ন প্রতিষ্ঠিত সূত্র ব্যবহার করে গণনা করা হয়। R , পাইথন, এক্সেল ইত্যাদির মতো আধুনিক সফ্টওয়্যার এ
z-stat গণনা করার জন্য ইনবিল্ট ফাংশন রয়েছে। z-stat এবং এর কিছু অন্যান্য সংস্করণ অনুমানের পরীক্ষার জন্য ভিত্তিক।
z-stat কী বা কোন অবস্থান দেখায় তা বুঝতে নীচের ভিডিওটি দেখার জন্য আমি আপনাকে দৃঢভাবে পরামর্শ দিচ্ছি।
R এ কীভাবে নমুনা করা হয় তা দেখতে, দয়া করে এই ভিডিওটি দেখুন।