ডেটা সংক্ষিপ্ত করার আরও উপায়
অবস্থান
প্রায়শই, ডাটার বৈশিষ্ট্য প্রকাশ করার জন্য প্লট প্রদর্শন করা সম্ভব হয় না । এই ক্ষেত্রে আমাদের আরও কিছু উপায় প্রয়োজন। আগের লেখায় আমরা পড়েছি যে , হিস্টোগ্রাম দিয়ে আমরা বিভিন্ন প্রশ্নের উত্তর দিতে পারি । যেমন বেশিরভাগ শিক্ষার্থীর ওজন কি 60 কেজির নিচে? বা , সর্বনিম্ন ওজন কোনটি , ইত্যাদি । গ্রাফ না এঁকে ও কিছু তথ্য অন্য উপায়ে পাঠকদের কাছে পৌঁছে দেওয়া যেতে পারে। এগুলি হল অবস্থান এবং আকার।
কেন্দ্রিয় অবস্থান
সম্ভবত সর্বাধিক ব্যবহৃত কেন্দ্রীয় অবস্থান হলো গড়। আপনার কাছে যদি 1000 শিক্ষার্থীর ওজনের ডেটা থাকে এবং আপনি এই সমস্ত ওজনকে একটি সংখ্যা হিসাবে জানাতে চান সেই ক্ষেত্রে কেন্দ্রীয় অবস্থানটি প্রযোজ্য । সুতরাং, যখন আমরা একটি নমুনা বা জনসংখ্যার প্যারামিটার উপস্থাপন করতে একটি নম্বর বা মান ব্যবহার করি (যেমন 1000 শিক্ষার্থীর ওজন) তখন আমরা কেন্দ্রীয় অবস্থান ব্যবহার করি।
সর্বাধিক ব্যবহৃত কেন্দ্রীয় অবস্থান হ’ল গড়। গড় গণনা করতে, সমস্ত মান যুক্ত করা হয় এবং তারপরে সেটি যেকটি সংখ্যা যুক্ত করা হয়েছিল , সেই সংখ্যা দিয়ে বিভক্ত করা হয়।
\[ \mu =\frac{\sum_{i = 1}^{n}{(x_i)}}{n} \] যেখানে \(\mu\) মানে গড় \(x_i\) মানে সংখ্যা গুলি \(n\) হলে যতগুলি সংখ্যা আছে
অর্থ্যাৎ যদি 10 টি সংখ্যা 1,2,3,2,5,4,3,6,5 এবং 6 হয় তবে তাদের গড় হলো
\[ \frac{(1+2+3+2+5+4+3+6+5+6)}{10} = 3.7 \]
R এ , এটি গণনা করার জন্য mean নামে একটি ফাংশন রয়েছে। উপরে বর্ণিত সংখ্যাগুলির গড় গণনা করার কোডটি নীচে দেখানো হয়েছে।
mean(c(1,2,3,2,5,4,3,6,5,6))## [1] 3.7আমরা যদি এই সংখ্যাগুলির ওপর আরও কিছু সংখ্যা যোগ করি , যেগুলি এই সংখ্যাগুলির থেকে খুব একটা বেশি বড়ো বা ছোট না , তাহলে নতুন গড় টি আগের গড় এর কাছাকাছি এক সংখ্যা হবে । যেমন, নীচে আমি ২,৪ আর ৭ যোগ করেছি ।
mean(c(1,2,3,2,5,4,3,6,5,6,2,4,7))## [1] 3.846154নতুন গড়টি আগে গণনা করা গড় থেকে খুব বেশি দূরে নয়।
তবে, আমরা সিরিজটিতে বিদ্যমান নম্বর থেকে বেশি বড় বা ছোট একটি সংখ্যা যুক্ত করলে জিনিসগুলি পরিবর্তন হতে পারে।
mean(c(1,2,3,2,5,4,3,6,5,6,12))## [1] 4.454545এই ক্ষেত্রে আমরা একটি নম্বর যুক্ত করেছি (12) এবং গড় বেড়ে ৪.৪৫ হয়ে গেছে । সুতরাং, কেবলমাত্র একটি উচ্চ মানের বা নিম্ন মানের উপস্থিতি গড় কে পাল্টে দিতে পারে । এটি প্রায় ই ঘটে পারে এবং তাই গড় খুব বলিষ্ঠ না। এবং গড় ব্যবহারের সময় অবশ্যই একটি সতর্কতা অবলম্বন করা উচিত।
আর একটি কেন্দ্রীয় অবস্থান পরিমাপ, যা গড়ের চেয়ে বেশি শক্তিশালী সেটি হ’ল মিডিয়ান। সংখ্যা গুলি কে ছোট থেকে বড় রূপে সাজানোর পর , সবচেয়ে মাঝের সংখ্যা টি হলো মিডিয়ান।
যদি সংখ্যা গুলির পরিমান বিজোড় সংখ্যা হয় তখন ফর্মুলা হলো
\[ median(x)=x_{(n+1)/2} \]
সুতরাং যদি 5 টি সংখ্যা 1,2,3,2 এবং 5 হয় তবে আমরা তাদের ছোট থেকে বড়ো সাজাবো । এটি 1,2,2,3,5 হয়ে যায়। 5 টি সংখ্যা আছে। সুতরাং n = 5 এবং n + 1 = 6। (n + 1) / 2 = 3। সুতরাং, মিডিয়ান হলো তৃতীয় সংখ্যা।
যদি সংখ্যা গুলির পরিমান জোড় সংখ্যা হয় তখন ফর্মুলা হলো
\[ median(x)=\frac{x_{n/2}+x_{(n/2)+1}}{2} \]
সুতরাং, যদি 6 টি সংখ্যা 1,2,3,2,5 এবং 4 হয় তবে আমরা প্রথমে তাদের ছোট থেকে বড় করে সাজাবো । এটি 1,2,2,3,4,5 হয়ে যায়। 6 টি সংখ্যা আছে। সুতরাং, n = 6 n / 2 = 3 এবং (n / 2) + 1 = 4। তৃতীয় এবং চতুর্থ সংখ্যাগুলি 2 এবং 3. মেডিয়ান হলো (2 + 3) /2=2.5।
R এ , এগুলি গণনা করার জন্য median নামে একটি ফাংশন রয়েছে।
median(c(1,2,3,2,5,4))## [1] 2.5ভেরিয়েবলে যদি সংখ্যা না হয় তখন কী হবে? আমরা কেন্দ্রীয় অবস্থানটি কীভাবে পরিমাপ করব? সেই ক্ষেত্রে , আমরা মোড ব্যবহার করে করি। মোড মানে যে পর্যবেক্ষণটি সবচেয়ে বেশি বার উপস্থিত । এটি সংখ্যাগত ভেরিয়েবলের জন্যও বৈধ। আমরা সংখ্যার উপস্থিতি (কত বার ) গুনে পরিমাপ করতে পারি। অথবা, আমরা বিন তৈরি করতে পারি (উদাহরণস্বরূপ, 1-5, 6-10 এবং তাই) এবং উপস্থিতি পরিমাপ করতে পারি।
1,2,3,2,5 এবং 4 সংখ্যা গুলির মধ্যে , 2 থাকে সর্বাধিক সংখ্যক বার উপস্থিত । সুতরাং, 2 হলো এই ভ্যারিয়েবল এর মোড। এক ই ভাবে a, b, c, a, c, a, b র মোড হলো a কারণ এটি সর্বাধিক সংখ্যক বার উপস্থিত । একটি নমুনায় (ভ্যারিয়েবল ) একাধিক মোড থাকতে পারে।
R এ মোড গণনা করার জন্য কোনও ইনবিল্ট ফাংশন নেই। তবে, আপনি নিজে একটি ফাঙ্কশন লিখতে পারেন।
mode.cal <- function(x) {
unique.x <- unique(x)
unique.x[which.max(tabulate(match(x, unique.x)))]
}
mode.cal(c(1,2,3,2,5,4))## [1] 2এগুলো ছাড়াও আরও দুটি ভাবে কেন্দ্রীয় অবস্থান বোঝানো যায় ।
জ্যামিতিক গড় (জিওমেট্রিক মিন ) বৃদ্ধির (গ্রোথ ) কেন্দ্রীয় অবস্থান বোঝার জন্য ব্যবহৃত হয়। উদাহরণস্বরূপ, যদি টানা তিন মাসে কোনও শেয়ারের দাম 1%, 1.5%, 4% বৃদ্ধি পেয়ে থাকে, তবে গড় বৃদ্ধি জ্যামিতিক গড় দ্বারা গণনা করা হয়।
\[ GM=\sqrt[n]{x_1\times x_2\times x_3 ... x_n} \]
অন্যটির ওয়েটেড মিন (Weighted Mean ) যা ব্যবহৃত হয় যখন বিভিন্ন পর্যবেক্ষণের আলাদা ওজন(Weight ) থাকে তখন । উদাহরণস্বরূপ, 10 ঘন্টা কাউকে নিয়োগের ব্যয় 100 । একই ব্যক্তিকে 6 ঘন্টা ভাড়া নেওয়ার ব্যয় 80 এবং 2 ঘন্টার জন্য 20 হয়। তখন প্রতি ঘন্টা গড় ব্যয় এই ভাবে গণনা করা হয়
\[ \frac {{100 \times 10} + {80 \times 6} + { 20 \times 2}}{10+6+2} \]
সূত্রটি হ’ল
\[ {Weighted} \space {\bar x} = \frac {\sum{f_i \times x_i}}{\sum f_i} \]
জ্যামিতিক গড়টি R এ এই ভাবে গণনা করা হয়
# growth of 1% means new value is 1.01 (i.e. 1 + 1%)
x<-c(1.01,1.015,1.04) # Stock price increased 1%, 1.5% and 4%
exp(mean(log(x)))## [1] 1.021583ওজনযুক্ত গড় গণনা করা হয় R এ weighted mean ফাংশন ব্যবহার করে। দুটি ভেক্টর ইনপুট হিসাবে সরবরাহ করা হয়। প্রথমটির মান এবং দ্বিতীয়টির ওজন(weight )।
cost<-c(550,420,800)
hour<-c(8,6,2)
weighted.mean(cost, hour) ## [1] 532.5অ-কেন্দ্রীয় অবস্থান
কেন্দ্রীয় অবস্থান পর্যবেক্ষণগুলির বর্ণনা করে। তবে বিতরণের বৈশিষ্ট্যগুলি বোঝার আপনার প্রায়শই বেশি প্রয়োজন হয় । যদি গড় কোনও কেন্দ্রীয় নম্বর সরবরাহ করে তবে আমরা এর চেয়ে আরও বেশি জানতে চাই। কোন মানের নিচে নিচের ২৫% পর্যবেক্ষণগুলি আছে; এই জাতীয় প্রশ্নের ক্ষেত্রে আমরা কোয়ার্টাইলস এবং পারসেন্টাইল ব্যবহার করি। কোয়ারটাইল এমন পরিমাপ যা চারটি সমান অংশে (পর্যবেক্ষণের সংখ্যার ভিত্তিতে) অর্ডার (ছোট থেকে বড় সাজানো ) করা ডেটা কে বিভক্ত করে।
25% পর্যবেক্ষণগুলি সর্বনিম্ন মান এবং প্রথম কোয়ার্টাইলের (Q1) মধ্যে থাকে, আরও 25% Q1 এবং Q2 এর মধ্যে থাকে। Q2 মধ্যস্থলে পর্যবেক্ষণ বা 50% পার্সেন্টাইল সংজ্ঞায়িত করে। সুতরাং, এটি median ।
Quartiles
কোয়ারটাইলগুলি quantile ফাংশনটি ব্যবহার করে র এ গণনা করা যায়। এটি প্রথম প্যারামিটার হিসাবে মানগুলির ভেক্টর গ্রহণ করে। এরপরে এর জন্য প্যারামিটার probs প্রয়োজন হয় যেখানে আপনি পার্সেন্টাইল নির্দিষ্ট করতে পারেন। Q1 এর জন্য, আপনি 0.25 (25%) প্রবেশ করতে পারেন। আপনি বিভিন্ন percentile এর একটি ভেক্টর সরবরাহ করতে পারেন। উদাহরণস্বরূপ c (0.25,0.5,0.75)।
quantile(c(1,2,3,4,5,6), c(0.25,0.5,0.75))## 25% 50% 75%
## 2.25 3.50 4.75আপনি এটি ব্যবহার করে যে কোনো পার্সেন্টাইল (0 থেকে 100) এর মান খুঁজে পান, যেমন 25 তম পারসেন্টাইল Q1, 50 তম Q2 উত্তর ইত্যাদি।
তথ্যএর বিস্তার(Spread)
পর্যবেক্ষণগুলি বিস্তার, data কতটা ছড়িয়ে তা নির্দেশ করে। এটি কেন্দ্রীয় অবস্থান পরিমাপের উপর আমাদের আত্মবিশ্বাসকে প্রভাবিত করে। যদি একটি পর্যবেক্ষণের গড় 20 হয় এবং পর্যবেক্ষণের পরিধি 19 এবং 21 এর মধ্যে হয় (সমস্ত পর্যবেক্ষণ 19 এবং 21 এর মধ্যে থাকে), আমরা পর্যবেক্ষণের গড়এর উপস্থাপনের উপর খুব আত্মবিশ্বাসী হতে পারি। তবে, পরিধি যদি -20 থেকে 100 হয় তবে আত্মবিশ্বাস দুর্বল হয়।
পরিসর ন্যূনতম এবং সর্বাধিক মান (উভয় সমেত) নির্দেশ করে যার মধ্যে পর্যবেক্ষণের সমস্ত মান রয়েছে। আমরা এটি গণনা করতে R এ রেঞ্জ ফাংশনটি ব্যবহার করতে পারি।
range(c(1,2,3,4,3,5,3,6))## [1] 1 6ভ্যারিয়েন্স, গড় থেকে পর্যবেক্ষণগুলির দূরত্ব (বর্গ) নির্দেশ করে। এটি পর্যবেক্ষণ এবং গড়ের মাঝে দূরত্বেগুলির বর্গের গড়।
\[ s^2 = \frac {\sum (x_i - \bar {x} )^2}{n-1} \] \(s^2\) হলো ভ্যারিয়েন্স \(\bar x\) হলো গড় \(n\) পর্যবেক্ষণ সংখ্যা(Number of Observations)
বর্গটি ঋণাত্মক সংখ্যা (Negative Number) এড়াতে ব্যবহৃত হয়। যখন আমরা এই সংখ্যা বা ভ্যারিয়েন্স এর বর্গমূল নিই, তখন আমরা স্ট্যান্ডার্ড ডেভিয়েশন পাই।
R এ ভেরিয়েন্সটি var ফাংশন ব্যবহার করে গণনা করা হয় এবং sd ফাংশন ব্যবহার করে স্ট্যান্ডার্ড ডেভিয়েশন গণনা করা হয়।
এখন ধরুন আপনার কাছে দুটি নমুনা রয়েছে এবং আপনি বুঝতে চান যে কোনটির বেশি ভ্যারিয়েন্স রয়েছে। একটি নমুনা মিটার এ এবং অন্যটি সেনটিমিটার এ । একটি দৃঢ় উদাহরণ তৈরি করতে আসুন আমরা সমান মান গ্রহণ করি। আমরা সেনটিমিটার এ একটি নমুনা নেবো। আর মিটার এ আরও একটি নমুনা নেবো । দ্বিতীয় নমুনা বা পর্যবেক্ষণ এর ম্যান গুলো প্রথমটি থেকে রূপান্তরিত । মানে সেনটিমিটার এর মান গুলো মিটার এ করা ।
in.cm<-c(100,200,300,400)
in.m<-c(1,2,3,4)
c(sd.cm=sd(in.cm), sd.m=sd(in.m))## sd.cm sd.m
## 129.099445 1.290994মজাদার! ইউনিটগুলির (সেনটিমিটার ও মিটার )পার্থক্যের কারণে একই মান এর বিভিন্ন স্ট্যান্ডার্ড ডেভিয়েশন দেখা যায় । কম সংখ্যক নমুনা বা রূপান্তরযোগ্য ইউনিট হলে , এটি তবুও সামলানো যায় । তবে অ রূপান্তরযোগ্য ইউনিটগুলির সাথে (উদাহরণস্বরূপ কেজি, মি।) এটি একটি সমস্যা হয়ে উঠতে পারে। এই জাতীয় নমুনাগুলির ভ্যারিয়েন্স তুলনা করতে আমরা কোইফিসিয়েন্ট অফ ভ্যারিয়েন্স ব্যবহার করি। এটি শতাংশে দেওয়া হয় এবং মান দ্বারা স্ট্যান্ডার্ড ডেভিয়েশন ভাগ করে গণনা করা হয়।
উপরের উদাহরণ থেকে গণনা করা যাক।
c(cov.cm=sd(in.cm)/mean(in.cm), cov.m=sd(in.m)/mean(in.m))## cov.cm cov.m
## 0.5163978 0.5163978উভয়ের কোইফিসিয়েন্ট অফ ভ্যারিয়েন্স হুবহু এক !
স্কিউনেস
স্কিউনেস সাংখিক উনিমডাল1 ভ্যারিয়েবল এর বিতরণ নির্দেশ করে । এটি তিন প্রকারের হয় যা নিচের চৰি তে বোঝানো আছে ।
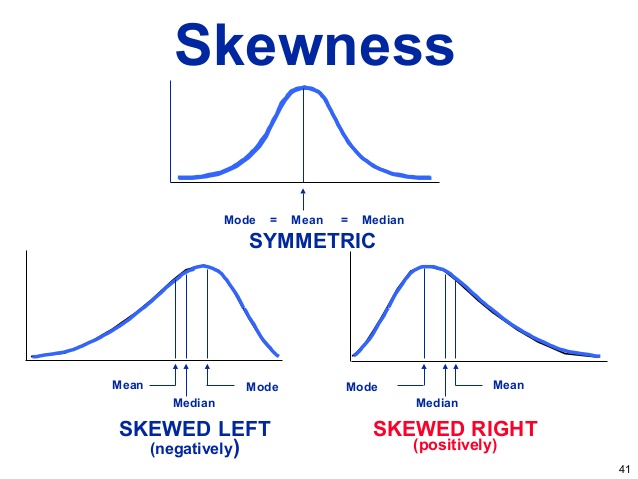
ক্রেডিট: ডগলাস কলেজ লার্নিং সেন্টার
গড়, মিডিয়ান এবং মোড এবং তুলনা করা বা গ্রাফ এঁকে গণনা করা ছাড়াও, পিয়ারসনের স্কিউনেস কোইফিসিয়েন্ট ব্যবহার করে স্কিউনেস খুঁজে পাওয়া যায় । এটি R এর moments লাইব্রেরি থেকে skewness ফাংশন ব্যবহার করে গণনা করা যেতে পারে।
moments::skewness(rnorm(100))## [1] 0.1466022যখন পিয়ারসনের স্কিউনেস কোইফিসিয়েন্ট 0 র সমান বা 0 হয় তখন বিতরণটি প্রতিসম (Symmetric Distribution ) হয়। 0 এর কম হলে এটি নেগেটিভলি সিমেট্রিক হয়। এবং যখন 0 এর বেশি হয়, তবে এটি পজিটিভলি সিমেট্রিক হয়।
সম্পর্কিত ভিডিও নীচে সংযুক্ত করা হয়েছে ।
Footnote
যে ভ্যারিয়েবল এর একটি মোড আছে↩︎